People have a strong emotional reaction when they find out that I'm a professor of mathematics education. Everyone—from neighbors, to hairdressers, to people I meet while shopping—is quick to declare that they were never very good at mathematics. I like to respond by posing a simple math problem (e.g., 27 + 25). After they solve the problem, I ask, "How did you solve it?" Without fail, this question is met with surprise as the person struggles to account for their mental processes—a challenge that is exacerbated by damaging beliefs that suggest the goal of mathematics is to recall and apply correct procedures rather than think deeply about what you are doing and why.
Metacognition, as defined by psychologist John Flavell, is "one's knowledge concerning one's own cognitive processes and products, or anything related to them … [and] the active monitoring and consequent regulation and orchestration of these processes (1976, p. 232). In other words, metacognition consists of both being aware of one's own thought processes (knowledge of cognition) and having the ability to control and influence these processes (regulation of cognition). However, what does this have to do with mathematics?
The Role of Metacognition in Problem-Solving
Despite the popular belief that mathematics is about memorizing and precisely following algorithms and procedures, mathematics is actually a subject of critical thinking, problem-solving, and creativity (Boaler, 2016, 2019). Given that problem-solving is, by definition, the process of working towards a goal to which solution is not immediately evident, it is crucial that problem solvers are not only aware of what they are doing and why they are doing it, but also have the ability to regulate these processes. For example, a seminal framework coined by mathematician George Pólya (1945/2014) suggested that problem-solving was a process of understanding a problem, creating a plan for solving the problem, carrying out the plan, and then reflecting on the answer and the process (see figure 1).
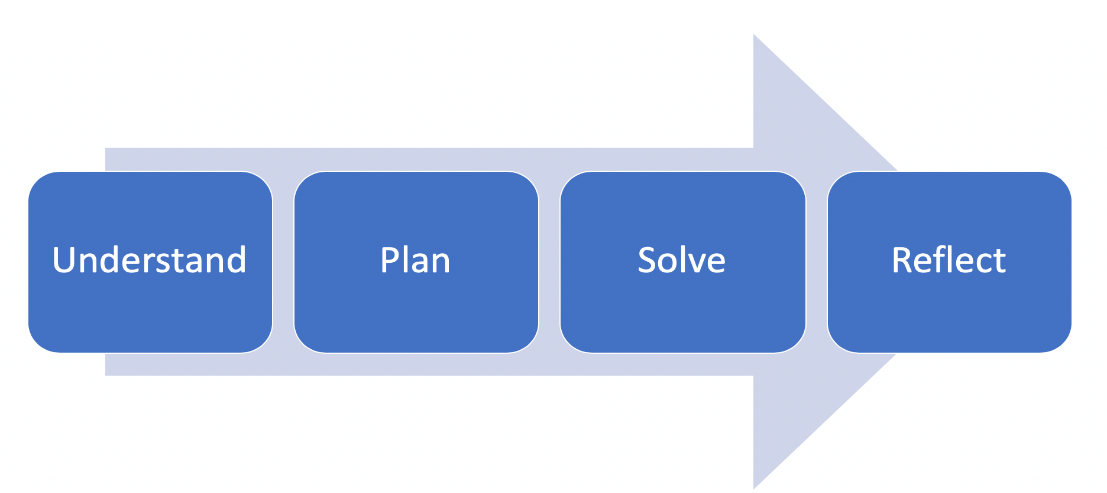
Figure 1. A visual representation of Pólya's problem-solving framework.
Throughout these four phases, metacognition plays an essential role in problem-solving as students make and regulate their thinking and their decisions. After all, if students are unaware of what they are doing and why they are doing it, they are unlikely to pinpoint causes of struggle when solving the problem and be able to work around stumbling blocks.
Metacognitive Awareness and Regulation
When a student first approaches a problem, success hinges on their ability to maintain an awareness of what decisions they are making and why they are making them. For example, students must first decide which heuristic(s), or strategies for solving a problem, to use by predicting which ones are most likely to successfully lead to a solution. Within this, students failing to use metacognitive awareness to guide their decision making may simply choose strategies and/or algorithms based on convenience or familiarity rather than on an analysis of the specifics of the problem.
Students must then determine how to apply their chosen heuristic to the given problem. If a student chooses to draw a picture, for instance, the student must consider what type of picture to draw and how to use the picture to model or solve the problem. Although drawing pictures is often thought of as a strategy that leads to solution pathways, pictures may also be used to help a student develop a better understanding of the problem itself—even when they do not directly result in a pathway towards a solution. Thus, without an awareness of how they are using the picture, students may overlook their increased understanding of a problem and may simply give up after their picture failed to lead to a solution.
Once a student has decided on a heuristic, however, they must continue to be aware of and monitor their progress. Such awareness is crucial in problem-solving because the student may realize that their chosen heuristic is not feasible within the given problem (e.g., drawing an entire scenario involving 1,000 people). Thus, students maintaining an awareness of their progress and thinking may realize that they need to find another heuristic (e.g., solving a simpler case) to utilize in conjunction with their chosen heuristic (drawing a picture).
As a second example, students maintaining an awareness of their thinking during problem-solving may also realize that the heuristic chosen is not yielding progress in terms of solving the problem and they may, therefore, revise their plan and/or choose another heuristic altogether. This awareness is crucial in that the problem-solving process is rarely as linear as suggested by figure 1. Rather, students may oscillate back and forth between phases (e.g., students may move from attempting to solve the problem back to revising their plan). In fact, many students will even begin solving a problem only to realize that they had not fully understood it initially and may, therefore, return to the understand phase in Pólya's process. At this point, a final advantage of having maintained metacognitive awareness throughout the problem-solving process surfaces—the students who were aware of the decisions they made (as they were making them) are more likely to persist through the struggles of problem-solving as they are now able to revisit any or all of those decisions to alter or refine them.
Given the inherent complexity of problem-solving detailed above, students failing to employ metacognitive awareness and regulation will often fail to successfully solve a problem because they either persist with ineffective strategies, or simply give up when their first strategy fails to yield successful results. Thus, it is imperative that mathematics teachers offer myriad opportunities for students to develop an awareness of and regulate their own thinking.
Creating Opportunities for Metacognition to Flourish
Two ways of providing a student with opportunities to refine their knowledge and regulation of cognition in problem-solving are problem-solving journals and recording students problem-solving processes. In order to exemplify each of these processes, the Charlie's Gumballs problem, available in the CueThink Problem Bank (a web-based problem solving application) and authored by The Math Forum, was used to create a sample problem-solving journal and a record of student work:
Charlie has a giant bag of gumballs and wants to share them with his friends. He gives half of what he has to his buddy, Jaysen. He gives half of what's left after that to Marinda. Then he gives half of what's left now to Zack. His mom makes him give 5 gumballs to his sister. Now he has 10 gumballs left. How many gumballs did Charlie have to begin with?
Problem-solving journals—student-created records detailing their entire journey through solving a problem (including their decisions, mistakes, and revisions)—not only infuse writing into mathematics classrooms, but also allow students to continuously monitor and reflect upon their decisions. These journals can be digital, using a platform like CueThink, or traditional pencil and paper records. In a journal entry a student might, for example, detail how he sought to understand the problem, how he tried to solve the problem, how he changed the heuristics he was using when the first ones did not work, and how he eventually arrived at and checked a solution.
By recording his thinking and strategies, the student had to maintain metacognitive awareness as he solved the problem, and this awareness provided him with insights that eventually allowed him to successfully solve the problem. Moreover, the journal can now also be used by both the student and the teacher to reflect on the problem-solving process and as launching points for class discussions on the problem and the rich mathematics that lies at its core. Thus, the problem-solving journal serves as a powerful vehicle for metacognition both during and after the problem-solving process.
Recording Student Thinking
As a second example, teachers can record students as they solve problems. For example, this video of a student solving the Charlie's Gumballs problem in CueThink showcases a student explaining exactly how they solved the problem and why they made certain decisions (e.g., where to start the number line). As with the journal, this recording not only forces students to deeply consider what they are doing as they solve a problem, but also allows teachers and students to reflect on and refine their understandings of problem-solving after completing the problem. By intentionally selecting videos to show to the class, teachers can use student thinking to drive instruction and can also focus class discussions on the vast role that metacognition plays in problem-solving.
Math Is Meta
Metacognition undergirds nearly every aspect of problem-solving. When students are presented with opportunities to monitor and regulate their thinking during problem-solving, they are not only refining their metacognitive skills, but may also even be more successful in solving the problem. While student journals and recording and discussing student thinking in applications such as CueThink are two methods of accomplishing this, teachers are encouraged to go beyond these methods and find other ways of enhancing student metacognition in mathematics. After all, it's the question—How did you solve it?—and not the answer that is at the heart of mathematics learning.




