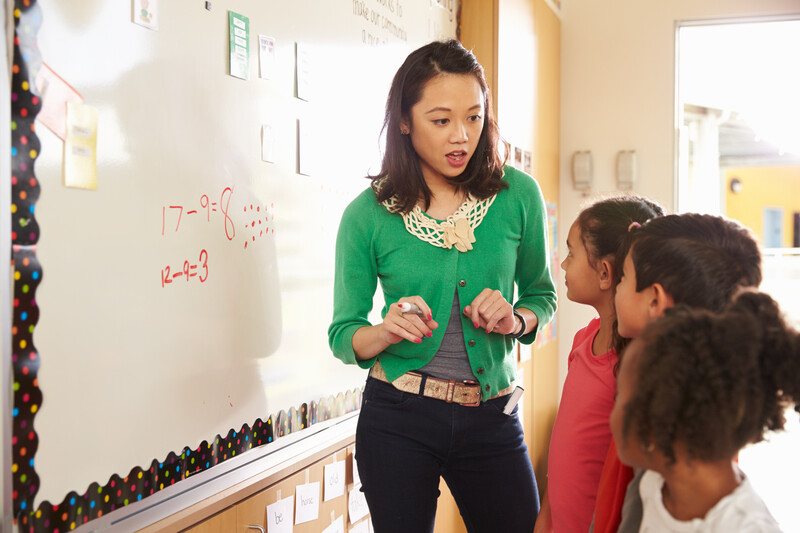One morning during the daily calendar routine, Ms. Baxter asks her 1st graders to think of a variety of ways to express the number of the day—12. Her exuberant students come alive with ideas to share. One child suggests 6 + 6, another 10 + 2. Others suggest 2 + 2 + 2 + 2 + 2 + 2 and 5 + 5 + 2. Finally, another one proposes 11 + 1. Ms. Baxter writes each expression on the whiteboard.
The next day, she writes 12 = ___ + ___ on the board and asks the students to recreate their thinking from the day before. Expecting a flurry of hands, Ms. Baxter is surprised when her students' faces show puzzlement. "You wrote it wrong," one child says. "It's backward," says another. More comments follow: "Put the 12 on the other side." "You can't write the answer first!"
Ms. Baxter is now the one looking puzzled, and she's faced with a teaching decision. Should she just rewrite the sentence in the more familiar format (___ + ___ = 12) and avoid this confusion? Should she tell the students that writing an equation this way is perfectly acceptable? Should she ask them more questions to find out why this form of the equation is so bothersome to them? Should she ask them what the equal sign means? Which of these instructional responses is most aligned with the concepts that 1st graders are expected to understand in the Common Core State Standards for Mathematics?
As teachers in classrooms across the United States put the new mathematics standards into practice, they'll face countless situations like this one. When teachers encounter an unexpected response or question from students, they must make an instant decision about the significance of the question and choose their response accordingly. The true success of the implementation of the new math standards will be measured here, in the innumerable minute-by-minute decisions that teachers make during instruction. Much attention has been focused on helping teachers use the new standards to plan lessons and units, but teachers also need to understand the intent and trajectory of the standards to capitalize on teachable moments in ways that support students' mathematical understanding and reasoning.
These new standards are not intended to be new names for old ways of doing business. For many teachers, meeting the standards will require a major shift in their approach to mathematics instruction, away from rote memorization and toward understanding and reasoning.
In our work with student teachers, we've found that teachers are better positioned to make instructional decisions that build a foundation for students' mathematical success when they recognize the key concepts in the standards, even when these concepts surface at unexpected times. Let's look at some essential terms in the math standards, as well as at some instructional shifts that will promote understanding.
The Equal Sign
Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false. (1.OA.D.7)
The meaning of the equal sign might seem obvious. After all, it's one of the first symbols that children encounter when learning about operations. However, its ubiquitous presence can lead to misunderstandings about its meaning, as illustrated in the opening vignette. Students often interpret the equal sign to mean "the answer is."
For example, when students are asked to answer 5 + 6 = ___, they may interpret the equal sign as the signal to write the solution in the blank. However, its meaning is much more robust. It means "is the same as" and expresses a numerical relationship. When students recognize the equal sign as a relational sign, it lays the foundation for future mathematical learning. With this understanding, statements like 8 = 3 + __ and 4 + 2 = 5 + __, and later, x + 5 = 11 − x make sense and open the door to new strategies for solving complex problems.
Why this concept is important. Understanding that the equal sign signals a relationship between quantities, that it isn't just a prompt to "give the answer," has been shown to offer lasting benefits as students move into the more abstract areas of mathematics in algebra and beyond (Knuth, Stephens, McNeil, & Alibali, 2006). Teachers can use discussions like the one described in the opening vignette to uncover misconceptions about this symbol and address them before they become an impediment to future learning. Engaging in frequent discussions about the symbol and its meaning in the early grades is crucial because developing a comprehensive understanding of the equal sign is a complex process that happens over time, not in a single lesson (Carpenter, Franke, & Levi, 2003).
How you can enhance it. Primary grade teachers can help pave the way for a smooth transition into algebra by making two shifts in their day-to-day practice.
First, from the time you introduce the equal sign, use language to expand students' understanding of it. Replace equals with synonyms such as is the same as, has the same value as, balances, or is worth the same as. Make a poster with the equal sign in the center and a web of synonyms around it, and include a drawing of a balance scale or teeter-totter as a visual reminder. Keep this poster in a prominent place as a reminder for students to use a wide range of terms as they build a deep understanding of the symbol.
Second, make sure that students are regularly exposed to number sentences that vary the position of the equal sign. Review your instructional materials. If the equal sign is always shown in the same position, rewrite some of the number sentences to ensure that students build a flexible and robust understanding of the symbol.
Cardinality
Understand the relationship between numbers and quantities; connect counting to cardinality. (K.CC.B.4)
Young children can "count" objects by mimicking the counting actions they've seen others do long before they understand that counting tells us important information—how many we have. Picture this: The teacher hands a kindergartner seven cubes and says, "Count these for me." The child touches each cube once, saying the next number in the count sequence, ending with seven.
Can the teacher conclude that this child understands counting? In fact, it's impossible to know without asking the child one final question: "How many cubes are there?" The child who responds "seven" understands that the last number in the sequence has special meaning—it tells the cardinality of the collection, how many are in it. A child who hasn't yet developed the concept of cardinality won't be able to answer the question and will often assume it's a cue to replicate the same counting actions that he or she just completed.
Why this concept is important. Cardinality is the ability to bring meaning to the counting process. It opens the door to using numbers for describing and comparing and lays the foundation for combining (adding) and separating (subtracting). Many of the early strategies children will develop for solving addition and subtraction problems rely on a meaningful understanding of counting (Clements & Sarama, 2009; Cross, Woods, & Schweingruber, 2009).
How you can enhance it. Two instructional shifts are helpful here. First, don't assume that a child's ability to recite numbers in order means that he or she comprehends counting and quantity. To find out, ask, "How many?" after each counting task, even when modeling those tasks. When taking the lunch count in the morning, count the raised hands—and then be sure to ask, "How many children ordered hot lunch today?"
A second shift is to approach early counting tasks with an eye toward addition and subtraction. Offer many opportunities for students to count a variety of objects in different-size sets and ask, "How many would we have if we combined these two piles of cubes?" and "How many would you have if I took two pencils out of your basket?" Such tasks encourage students to bring meaning to the counting process and use it as a strategy to solve more complex problems.
Properties
Apply properties of operations as strategies to add and subtract. (This skill appears in several 1st and 2nd grade standards.)
Working and thinking strategically are hallmarks of the new standards in math. This applies even to basic skills, such as computation with addition and subtraction. Using the commutative and associative properties, young children can make insightful calculation decisions that will simplify computation and reduce errors.
For example, when a student is faced with a problem like 6 + 7 + 4, a clever calculation move would be to rearrange the numbers by applying the commutative property (7 + 6 + 4) and regroup by applying the associative property (7 + [6 + 4]) to create a new problem that's much easier to solve. Teachers need to emphasize the concepts, not the terminology. In fact, the goal isn't to "teach" these properties at all, but rather to give students opportunities to observe patterns, identify relationships, and make their own generalizations about how numbers can and can't be manipulated for each operation (Carpenter et al., 2003).
Why this concept is important. Simplifying calculations isn't the only benefit of knowing and using properties. Mathematical Practice 7 states that "mathematically proficient students look closely to discern a pattern or structure." Students who develop a habit of mind for problem solving that includes reflection and planning ahead will be able to use this skill to great advantage throughout their mathematical careers. Students without this capacity have a tendency to plunge headlong into every problem without first taking a step back to identify the goal and consider multiple solution paths. Whether the context is single-digit addition or more advanced topics, making and using generalizations in clever ways to simplify seemingly complicated problems are essential problem-solving skills.
How you can enhance it. The primary instructional shift here is to create regular opportunities for students to make and test generalizations about numbers and operations. For example, pose a set of problems containing number pairs like 5 + 2 = ? and 2 + 5 = ? Observe students as they solve them, and watch for a student who immediately knows the answer to the second problem after solving the first. Ask this student to share his or her strategy with the class, and see who agrees or disagrees. Follow up with questions like, "Will this always be true, even for large numbers? How could we know for sure? Is this true for subtraction, too?"
Given the chance to observe and discuss pairs of numbers combined in "forward" and "backward" order, students will invariably come up with some version of a "turnaround" rule for addition—the commutative property—and will then use it to solve more complex problems. Remember that the practice of observing and generalizing is as important as knowing and using the properties. Encourage the exploration of a variety of student observations, even those that may prove to be false.
Composing and Decomposing
To compose means "to create or to build." To decompose means "to break down." The fact that these two verbs occur in six Common Core standards and across three mathematical domains in the K–2 standards is a strong indication of their importance.
Let's look at geometry to illustrate the concept. Students who can compose and decompose shapes have the ability to put geometric pieces together, take them apart, and—most important—put them back together in different ways (see fig. 1).
Figure 1. Decomposing and Recomposing Geometric Shapes
Several standards in the number domains use the terms compose and decompose to describe similar thinking applied to quantities. Consider the problem 27 + 19 = ___. A student who can compose and decompose numbers could solve this problem by breaking the numbers apart and putting them back together in convenient and clever ways (see fig. 2).
Figure 2. Decomposing and Recomposing Numbers
Why this concept is important. Students who develop flexible thinking about numbers early in their schooling are poised to develop complex mathematical thinking as they progress through the grades. Students who can decompose and recompose numbers see many options when presented with a challenging computational problem. Students without this ability typically have only one way to approach it: They line up the numbers vertically and follow a memorized procedure. The ability to compose and decompose numbers also enhances students' knowledge of place value and landmark numbers, such as 25 and 75, and potentially even their reasoning with negative numbers.
How you can enhance it. Use every opportunity to encourage flexible thinking about numbers. Ask, "What's another way to think of that number? How could we break that number into simpler pieces?" Pose number riddles with clues like, "I'm thinking of a number that's made of 4 tens and 7 ones. What's my number?" Or, "If you take my number apart one way, you can see 25 and 25 and 5. If you take it apart another way, you can see 40 and 15. What's my number?" Emphasize finding combinations that use "friendly numbers," like decade numbers (multiples of 10), and easy referents, like 25 or 75.
To promote the geometric aspect of this concept, include shape puzzles as free-choice activities. You can even have students create and share their own puzzles. Research shows that the ability to compose and decompose geometric pieces transfers to flexibility with number combinations (Clements & Sarama, 2009), so be sure to provide experiences with shapes and numbers.
Unknowns
Use addition and subtraction within 20 to solve word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions. … (1.OA.A1)
Traditionally, the term unknown is associated with variables in algebra, but that's not the intent in this standard. The point here is to ensure that students go beyond solving the traditional, straightforward word problem formats so often found in textbooks.
For example, a problem like this is commonplace in 1st grade: "Dina had 12 marbles. She gave her cousin 7 marbles. How many marbles does Dina have left?" In this example, we can identify a starting amount (12 marbles); an amount of change (7 marbles); and a resulting amount (the unknown). By shifting the unknown to a different position, this problem could provide much more challenge. Consider these versions:
Result unknown: "Dina had 12 marbles. She gave her cousin 7 marbles. How many marbles does Dina have left?"
Change unknown: "Dina had 12 marbles. She gave her cousin some marbles. Now Dina has 5 marbles. How many marbles did Dina give her cousin?"
Start unknown: "Dina had some marbles. She gave her cousin 7 marbles. Now Dina has 5 marbles left in her bag. How many marbles did Dina have at the start?"
The second and third versions of the problem are more complex both linguistically and mathematically. By varying the position of the unknown, students are now required to generate and apply sophisticated problem-solving strategies.
Why this concept is important. Problems with unknowns in different positions promote multifaceted understandings of relationships among quantities and encourage the development of robust problem-solving skills. When children begin solving word problems, they typically use cubes, drawings, or fingers to represent and act out the situation. A "result unknown" problem (like the original marbles problem) lends itself to this strategy.
However, when the change or the start is unknown, the problem cannot readily be represented using materials or drawings. Students will have to try alternative strategies that involve advanced planning. Problems in which the change or start is unknown require students to combine their knowledge of number relationships and mathematical reasoning to generate more advanced strategies.
How you can enhance it. Shift the emphasis for solving word problems from a routine approach in which most of the problems follow a formula or pattern to one in which there's plenty of variation in the types of problems posed. Students will develop new solution strategies when they can't solve the problems using their original methods (Carpenter, Fennema, Franke, Levi, & Empson, 1999).
Review your curricular materials to see whether they include opportunities to solve problems that represent a wide range of types and structures. Keep in mind that it isn't necessary to rely solely on your instructional materials as the source for interesting and varied word problems. Teachers can create their own word problems by varying the number values and the position of the unknown and starring their favorite characters—themselves! There is great power in personalized problems, ones that are based in familiar contexts, such as our school, our class, and our families. If students feel a connection to the problem, they'll eagerly persevere with more challenging problems.
First, Understand
In a 2012 ASCD publication, the first on a list of recommendations for moving the implementation of the new standards forward is to "make sure educators deeply understand the standards and the key instructional shifts they require" (p. 31). Having a thorough understanding of the vocabulary and concepts in the standards provides a strong foundation for making sound instructional choices and will help teachers foster the critical-thinking, problem-solving, and analytical skills that students will need for future success.
<ATTRIB> Authors' note: The standards quoted in this article are from National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common Core Standard Standards for Mathematics. Washington, DC: Authors. Retrieved from www.corestandards.org/Math </ATTRIB>