Student work is the currency of the classroom. Every day, students in classes around the world produce massive amounts of work in the form of written assignments, projects, worksheets, and other products. But how can educators unlock the power of this rich source of data? How can we move the purpose of student work from proving mastery to improving learning? (Deuel, Nelson, Slavit, & Kennedy, 2009). Consider the following scenario of a traditional approach to looking at student work.
A team of 3rd grade teachers discusses student work produced during a math lesson about measuring area. In the activity, students were asked to compare the area of two rectangular robot heads and decide which one covered more area. The teachers talk about one student's response (see fig. 1). This student used a ruler to measure the height of the two heads and said, "The first one is two inches, and the second one is three inches, so the second one is bigger."
Figure 1. Robot Head Area Task
Jane facilitates the discussion about the student's work with three other teachers.
JANE: What do you notice about this student's work?ALICE: The student only measured the heights of the two heads.ROBERT: I noticed that the student knows how to use a ruler correctly, but he doesn't seem to understand the concept of area.ROSA: It was interesting that the student said the second head was "bigger" and didn't use the word "area."JANE: What do you think this student was thinking about?ROBERT: The student doesn't seem to understand that to compute area, you need to measure both the length and width of the shape and then multiply.ROSA: This student might not even know what "area" means.JANE: What would you do next in your instruction?ALICE: I would review the concept of area and emphasize that it is the amount of space inside of the shape. Comparing only the heights of the two shapes doesn't give you a comparison of the area.
This dialogue is consistent with the kinds of responses offered in formative assessment protocols. Although the teachers use the student's work to broadly identify what he knows and what feedback they can provide, this discussion is still hovering above the precise analysis needed to guide productive decisions about teaching and learning.
Incremental Learning
Learning progressions are a valuable tool that teachers can use to go beyond the traditional approach and unlock the potential of student work. Also referred to as "learning trajectories" in mathematics, learning progressions are described as "a carefully sequenced set of building blocks that students must master en route to mastering a more distant curricular aim. These building blocks consist of subskills and bodies of enabling knowledge" (Popham, 2007, p. 83).
A key idea behind learning progressions is that they are informed by research on how students learn and how students' thinking develops and becomes more sophisticated over time as a result of instruction. Learning progressions are distinct from educational standards; progressions describe the typical ways students think about a topic, whereas standards are aspirational statements based on expert consensus about what students should know and be able to do. Another common feature of learning progressions is that they describe the stages or levels students move through as their understanding develops, the kinds of tasks that students can perform at each level, and what that performance looks like (Heritage, 2013).
Learning progressions are ideal for interpreting student work. Although existing protocols on looking at student work engage teachers in reflection about what the work reveals about students' thinking, learning progressions can help teachers identify student work that illustrates different levels of developing expertise. In doing so, teachers can place student work along that continuum.
In 2014–2015, we worked with 22 3rd grade teachers in the United States and Australia as part of a research study to evaluate the insights that a learning progression provides about students. Specifically, we examined how familiarity with a learning progression increased teachers' ability to find evidence of students' level of thinking, and whether that knowledge helped teachers plan more targeted and personalized instruction.
The teachers participated in professional development (PD) that introduced them to a learning progression about area measurement and engaged them in several activities designed to interpret student work using the progression. Six teachers participated in 20 hours of face-to-face PD at their school, and the remaining 16 participated in online PD modules. Our results were quite promising. We found that the learning progression not only served as a useful framework for examining student work, but it also increased teachers' content and pedagogical knowledge for teaching area measurement. Here, we share an example from our project to illustrate how the learning progression can help teachers interpret student work.
Measures of Student Understanding
Geometric measurement of area is usually defined as covering or filling space and then quantifying that covering. As students develop area measurement skills over time, they typically display several misconceptions. For example, when students work on tasks that require them to cover space to measure area, they often leave gaps between units, overlap them, double count them, or combine units of different size (Clements, Sarama, & Battista, 1998; Lehrer, 2003). Moreover, it is often difficult to advance students from the strategy of counting or adding individual tiles in a figure to the more sophisticated strategy of using the row-and-column structure of a shape to compute area. The latter strategy leads to a conceptual understanding of the area formula, length times width (Baturo & Nason, 1996). The teacher plays an important role in helping students resolve these misconceptions—and eventually develop a full conceptual understanding of the area formula.
Figure 2 shows a task for measuring the area of a hippopotamus's living space. Students can use a variety of strategies to find the area, which, in turn, reveal the sophistication of their reasoning. The teachers in our study were asked to examine Thomas's response (see fig. 3), describe the student's thinking and misconceptions, and suggest an instructional activity.
Figure 2. Hippopotamus Area Task
Figure 3. Thomas's Response
Before participating in the professional development, teachers' descriptions and ideas for instructional responses tended to be vague. For instance, when asked to describe what Thomas knows and understands, the teachers described his strategy ("Thomas understands area by placing the shapes on the grid and counting the squares") rather than his underlying thinking. They provided very general instructional strategies, such as reviewing or reteaching the area formula.
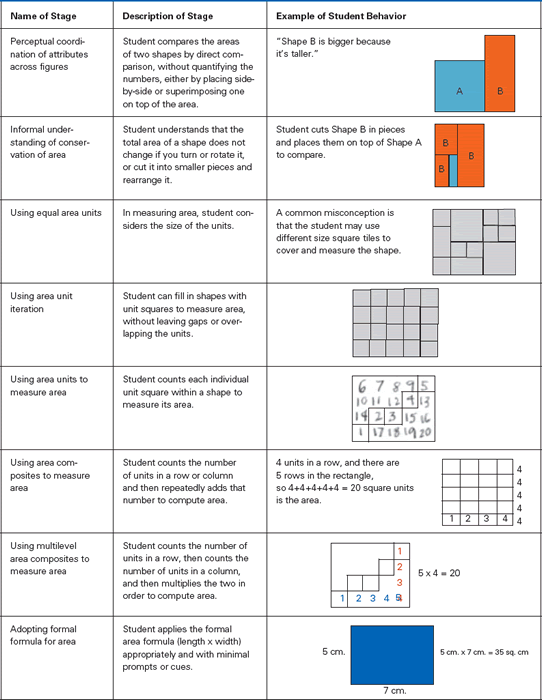
In contrast, the learning progression for measuring area specifically describes the process of student thinking and provides sample work at each level. Figure 4 presents some of the relevant stages of the learning progression we constructed. For students to acquire a full conceptual understanding of the area formula, they pass through a series of intermediate stages—each stage building on the previous one and preparing students for the next.
Figure 4. Excerpt of Learning Progression for Area Measurement
All figures copyright © 2015, Pearson Education, Inc., Research and Innovation Network. All rights reserved.
Using the learning progression as a framework, a teacher can see that Thomas's work provides evidence that his current thinking is consistent with the stage called "using area units to measure area." The next stage in students' learning of area measurement is "using area composites to measure area." At this next stage, students understand that a shape is made up of rows and columns and that a more efficient way to measure area involves use of the composites.
After completing the PD, the teachers in our study could interpret student thinking by referring to the intermediate stages of the learning progression. They were better able to help students like Thomas move from seeing area as a collection of individual units to understanding area as a collection of row and column composites. With those more sophisticated stages in mind, teachers gave specific instructional suggestions, such as working on composition and decomposition of shapes or giving students fewer blocks to measure area, to bridge the gap between the two stages and help students reach the next level.
A Look Back at the First Task
Looking back at the initial task of measuring the area of robot heads, if the teachers became familiar with the learning progression, their discussion of student work could be much more focused and informed, resulting in more concrete and targeted instructional suggestions.
JANE: What do you notice about this student's work?ALICE: The student only measured the heights of the two heads.ROBERT: The student knows how to use a ruler correctly, but he doesn't seem to understand that he needs to measure both height and width to compare area.JANE: What do you think this student was thinking about?ROBERT: The student seems to only consider height as a way to measure area. Isn't this a common misconception in the learning progression stage of "perceptual coordination of attributes across figures"?ROSA: Well, we are not sure about that. In the task, the two heads look as if they have the same width. Maybe the student noticed this, and that's why he measured only the height.ROBERT: True. We need to examine this student's thinking further with additional tasks.JANE: What do you think you might do next in your instruction?ROSA: I would give the student two shapes that have very different lengths and widths to determine whether he recognizes the two dimensions.ALICE: I would try to rotate the shapes and ask him to measure again.ROBERT: We could also ask him to cut the shapes and try to "fit" one into the other. That will help him to master the idea of "conservation of area."
Learner-Centered Practices
Our research shows that a learning progression can support teachers as they take a more fruitful look at student work and that they can use the insights gleaned as part of their ongoing formative assessment. In our project, teachers worked as a team to make meaning of the learning progression and to apply it to their daily practice. This approach is consistent with the idea of collaborative inquiry, which is critical for transforming teaching and improving student learning (Langer & Colton, 2005). And because the progressions are based on observations and insights from decades of research on students, learning progressions are naturally learner-centered. They take a developmental view to help teachers focus on individual students' learning over time and how they can assist that development.
Yet, despite recent attention to learning progressions as a potential tool to reform assessment and instruction, efforts to support teachers' use of these progressions are not prevalent. The barriers to widespread adoption include a lack of district resources to provide sustained professional development and misalignment of learning progressions with existing curriculum, assessments, and instructional materials. Close work with teachers as they are introduced to learning progressions and integrate them into practice is essential to fulfill their promise for helping teachers and ultimately students.