Within mathematics education, talk about "the NCTM Standards" is everywhere. But because different people focus on different aspects of the Standards developed by the National Council of Teachers of Mathematics (NCTM, 1989, 1991, 1995, in press) and may interpret them differently as well, what they mean by "the Standards" is not always clear.
NCTM released the first Standards document in 1989. This volume, which focused on curriculum, was followed in 1991 and in 1995 by teaching standards and assessment standards, respectively. In April 2000, NCTM will release Principles and Standards in School Mathematics, a revised document that makes more explicit the basic underlying assumptions of the original Standards documents. The central messages about high-quality mathematics teaching and learning remain unchanged. We refer to these documents collectively as "the Standards" or "the NCTM Standards."
New Views of Mathematics Learning
The Standards present a view of mathematics learning, teaching, and assessment that shifts the focus of curriculum and instruction. Whereas traditional mathematics education focuses on memorization, rote learning, and the application of facts and procedures, the Standards-based approach emphasizes the development of conceptual understanding and reasoning. A corresponding pedagogical shift has moved the focus from direct instruction, drill, and practice toward more active student engagement with mathematical ideas through collaborative investigations, hands-on explorations, the use of multiple representations, and discussion and writing. The educational perspective that views students as being actively involved in building their own understanding is often called "constructivist."
Mathematical literacy is essential if students are to become informed and competent citizens.
All students can and should become mathematically literate, not just students who have traditionally performed well in mathematics classes.
Literacy involves understanding mathematical principles; developing mathematical ways of thinking; and acquiring fluency with number, geometry, and data.
Students develop this literacy by actively doing mathematics, using their skills and knowledge to solve problems and to investigate mathematical ideas.
Many leading mathematics educators interpret the relatively poor showing of U.S. students in the Third International Mathematics and Science Study (TIMSS) as evidence of the need for a change toward Standards-based mathematics instruction as described in the NCTM documents. Educators argue that student performance on the TIMSS evaluation indicates a weakness in students' conceptual understanding and mathematical reasoning abilities and that one source of this weakness is the curriculum, frequently described as “a mile wide and an inch deep.”
Evaluating Standards-Based Curriculums
Curriculum developers have produced a number of mathematics curriculum programs specifically to help teachers interpret and implement the Standards. These developers have grounded their work in the aforementioned core beliefs, creating materials that will help teachers promote deeper and more substantial mathematical understanding in their students. The result is a collection of mathematics programs that bear a family resemblance to one another but that represent distinctive interpretations of the core beliefs.
Yet caution is in order. Teachers and administrators must be able to recognize materials that will promote the goal of creating rigorous, constructivist-based mathematical environments in which students develop both skills and deep understanding. Some programs that describe themselves as "Standards based" are not constructed around these core beliefs. Nonetheless, even a cursory examination confirms that most mathematics materials look different from those of 20, or even 10, years ago. All but the most traditional of today's textbooks offer sections on problem solving, include practical applications, and provide some opportunities for students to express their ideas.
Yet, just as a table made of solid wood differs from one that sports only a veneer, programs designed from the outset to embody the mathematical approaches and pedagogical principles advanced by the Standards differ significantly from those that have retrofitted some new activities and problems to an approach based primarily on teacher demonstration and student practice. What characteristics of curriculums can help educators distinguish between these approaches?
Mathematical Content
First and foremost, the NCTM Standards are about the ideas and skills that students should acquire during their K–12 mathematics education. The Standards stress the importance of helping students develop deep conceptual understanding relating to the major strands of mathematics (number and operation; patterns, functions, and algebra; geometry and measurement; and data analysis, statistics, and probability), acquire fluency with skill-based manipulations, and learn to reason and communicate about mathematical ideas. Rather than present mathematics as a set of discrete and unrelated topics that students learn, forget after the test, and then (perhaps) relearn the next year, these curriculums support students' development of robust mathematical understanding by requiring them to hypothesize, predict, observe, and reason about mathematical situations.
Standards-based curriculums focus on the big ideas in mathematics—those principles that govern the structure and functioning of the mathematical system. When students understand these big ideas, they have the conceptual tools to approach and solve many kinds of problems. One fundamental idea of algebra, for example, is that we can operate on an unknown number as if it were known. The ability to think about mathematical relationships in terms of the general case allows students to summarize observations, to make predictions, and eventually to develop formal proofs.
Some people have incorrectly interpreted the emphasis on conceptual understanding as a disregard for skill mastery. Nowhere do the Standards contend that computation is unimportant or that students can get by without knowing basic number facts and operations. They do, however, recommend diminishing the amount of class time dedicated to skills practice ("drill and kill") to make room for conceptual learning. Some of the current Standards-based programs embed the skill mastery in games or activities that also target other kinds of thinking, for example, developing strategic thinking or number sense. Because skill mastery is less overt in such contexts, a casual observer unaccustomed to identifying the skill component of Standards-based activities may have the impression that skills and facts are not being taught.
Mathematical Processes
Students gain mathematical competence by learning to work with mathematical ideas, to solve problems, and to communicate their ideas to others. The Standards maintain that curriculum programs should develop the following five mathematical processes:
Problem solving. Students use mathematically productive ways to approach problems, which include hypothesizing, building a variety of representations, abstracting, and making generalizations.
Reasoning and proof. Students think systematically and critically about mathematics by making observations, proposing and investigating conjectures, and developing mathematical arguments and proofs.
Communication. Students effectively organize and articulate their thinking, consider the ideas of others, and develop facility with the language of mathematics.
Connections. Students recognize the coherence of mathematics as a discipline by seeing interrelations among ideas and by understanding the power of mathematics through connections with outside disciplines and contexts.
Representation. Students develop and effectively use a repertory of representations to organize thinking and to model and interpret mathematical situations. (NCTM has added this process standard to its forthcoming Principles and Standards.)
By emphasizing these processes, the Standards stress that mathematical thinking develops through engagement in mathematical work. Chess Life Master John Collins talks about a "chessical" way of thinking—the ability to read a board, understand the flow of play, and command the interplay of strategy and tactic. Chess players learn to think chessically by grounding their study of the game in its play. Similarly, students develop mathematical knowledge and ways of thinking by grounding their study in mathematical inquiry and exploration.
Figure
Mathematics for All
Historically, mathematics has often been considered a subject understood by only a select and talented few. The Standards take a contrary view, emphasizing the importance of making mathematics accessible to all students—those who have traditionally excelled and those who have struggled or simply tuned out. The Standards call for engaging all students in educational experiences that will enable them to make sense of mathematics and to recognize and value the power of their own mathematical thinking.
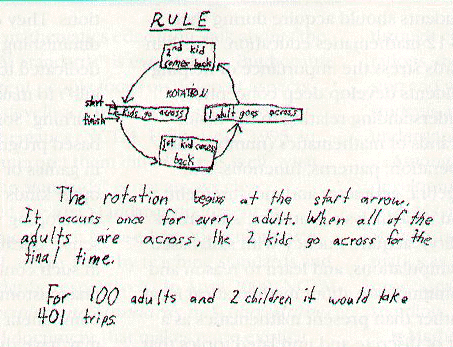
The developers of standards-based curriculums have addressed this issue by creating lessons with multiple entry points so that students with different levels of mathematical sophistication and different learning styles can engage with the mathematical ideas. Curriculum developers have also sought to motivate students to engage in mathematical work by presenting problem contexts that students are likely to find interesting and compelling. "Crossing the River" (fig. 1) is an example of a problem that engages students at a variety of levels.
Figure 1. Multiple Ways to Solve a Problem
Crossing the River
A group of 8 adults and 2 children needs to cross a river. A small boat is available that can hold 1 adult or 1 child or 2 children. Everyone can row the boat.
How many one-way trips does it take for them all to cross the river?
How many trips would it take for 2 children and 100 adults?
Student 1: It takes four trips to get 1 adult across the river. And one additional trip for the children to get across the last time. For 100 adults to get across the river, including 2 kids, it would take 401 total one-way trips.
Student 2: Begin with 3 trips to get 1 adult over. Each additional adult is four trips. For part B, subtract 1 from the total number of adults. Multiply that answer by 4. Add 3 to the total of that. Add 2 to get the kids across and there's your answer! (A − 1) x 4 + 3 + 2
Student 3: See diagram.
The first student describes a rule for counting the total number of trips. The second uses a traditional algebraic representation, and the third student describes the solution with a diagram and a written explanation.
A Different Kind of Mathematics Curriculum
Interact with a range of materials for representing problem situations, such as manipulatives, calculators, computers, diagrams, tables, and charts;
Work collaboratively as well as individually;
Discuss mathematical ideas; and
Focus on making sense of the mathematics they are studying as well as on learning to achieve accurate and efficient solutions to problems.
Standards-based materials take an integrated approach to topics from the earliest grades, with several areas of mathematics appearing at each grade level and developing connections to one another. Skill acquisition and practice are often embedded in a larger activity or are presented in a context other than pure drill. For example, in the elementary Everyday Mathematics program (UCSMP, 1998), games such as "Addition and Subtraction Top-It" allow students to practice their number skills and arithmetic facts (fig. 2).
Mathematical ideas reappear at different grade levels in increasingly sophisticated forms. For example, investigations of patterns at the elementary level lay a foundation for the study of algebraic relationships in the upper grades.
Mathematical knowledge is developed within both practical and conceptual contexts, with less emphasis on rote symbol or number manipulation. For example, the 9th grade unit "Testing 1, 2, 3" in the high school curriculum Mathematics: Modeling Our World (COMAP, 1998) uses the context of steroid and medical testing as the context for investigating the mathematical ideas of probability, optimization, modeling, and area.
Many problems are complex, involving a number of mathematical ideas and skills and requiring more time and thought to solve than the problems of the past.
The programs emphasize different kinds of representations, such as charts, tables, graphs, diagrams, and formal notation, for exploring, describing, and testing problem situations
Lessons employ less direct instruction and more student collaboration, conjecture, exploration, and discussion of mathematical ideas. Lessons extend over several days and involve student activity followed by class discussion.
Figure 2. A Skills Practice Game
Addition Top-It
Each player turns over two cards and calls out the sum. The player with the higher sum wins the round and takes all the cards. Play ends when not enough cards are left for each player to have another turn. The player with more cards wins.
Assessment tip: You might observe whether children rely on counting dots or using fingers to add the numbers. Children who have command of the addition facts will automatically call out the sum.
Note: Reprinted with permission from Everyday Mathematics: Second-Grade Teacher's Manual and Lesson Guide, Vol. A (Chicago: Everyday Learning Corporation, 1998).
These new curriculum programs offer teachers and students a blueprint for change in mathematics education by providing coherent, carefully researched, and academically rigorous courses of mathematical study. These programs are an important part of the educational equation for promoting a deeper and richer kind of mathematical learning for students.